Revolucionando la Modelización Financiera con IA. El modelo de Heston es uno de los modelos más utilizados en finanzas para describir la evolución de los precios de los activos. Fue desarrollado por Steven Heston en 1993 y ha sido ampliamente utilizado para la valuación de opciones. En este modelo, se asume que la volatilidad del activo subyacente es estocástica y está correlacionada con el precio del activo. El modelo de Heston es muy popular debido a su capacidad para replicar la sonrisa de volatilidad observada en los mercados financieros.

El efecto Zumbach es un fenómeno que puede ser observado en modelos de volatilidad estocástica, como el modelo de Heston. Fue descubierto por el matemático y físico suizo Gilles Zumbach en 2002, quien demostró que la tasa de crecimiento de la volatilidad implícita en las opciones depende de la tasa de interés libre de riesgo. Este efecto tiene implicaciones importantes en la práctica financiera, ya que puede afectar a la valoración de opciones y a la gestión de riesgos.

El artículo Deep calibration of the quadratic rough Heston model, realizado por Mathieu Rosenbaum y Jianfei Zhang, presenta una aplicación de redes neuronales para calibrar el modelo cuadrático rough de Heston. Este modelo es una extensión del modelo de Heston que tiene en cuenta el efecto de Zumbach.

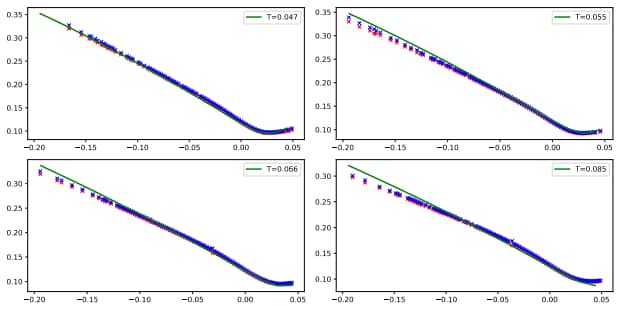
En la introducción del artículo se presenta el paradigma de rough volatility y se discute el modelo de Heston como un modelo popular en finanzas para describir la evolución de los precios de los activos. Se destaca la importancia del efecto Zumbach en el paradigma de rough volatility y cómo el modelo cuadrático rough Heston puede llenar esa brecha.

Los autores explican cómo el modelo se aproxima mediante factores múltiples y se utiliza una red neuronal para calibrar los parámetros del modelo. La red neuronal se entrena utilizando datos simulados para posteriormente discutir los resultados de la calibración. Los autores muestran que el modelo puede reproducir muy bien las volatilidades implícitas de los índices SPX y VIX y obtener precios de opciones VIX dentro del spread de oferta y demanda.

Finalmente, los autores explican cómo utilizar las redes neuronales entrenadas para coberturas con cálculo instantáneo de las cantidades de cobertura. Se discuten algunos ejemplos de simulaciones para demostrar cómo la red neuronal se puede utilizar para la cobertura de opciones.

El artículo presenta una aplicación interesante de las redes neuronales para calibrar el modelo cuadrático rough Heston. Los autores demuestran que el modelo puede reproducir muy bien las volatilidades implícitas de los índices SPX y VIX y obtener precios de opciones VIX dentro del spread de oferta y demanda. También se demuestra cómo utilizar las redes neuronales entrenadas para la cobertura con cálculo instantáneo de las cantidades de cobertura.

La utilización de técnicas de inteligencia artificial como las redes neuronales puede contribuir a mejorar la eficiencia y efectividad de los modelos financieros utilizados en la práctica financiera. La combinación de modelos como el modelo de Heston y el uso de redes neuronales puede dar lugar a mejores predicciones y a la obtención de mejores resultados en la gestión de riesgos y en la toma de decisiones de inversión.

En este sentido, una herramienta como AInvestor se beneficia de la utilización de redes neuronales para mejorar la optimización de portafolios y carteras, procesando las cadenas de opciones para obtener una mejor distribución del riesgo y las expectativas de mercado que componen los portafolios a optimizar. Combinar la optimización tradicional con dichas expectativas es uno de los pasos más importantes a la hora de generar un portafolio robusto que no se base únicamente en datos históricos.